گام به گام فعّالیت صفحه 2 درس 1 ریاضی نهم (مجموعه ها)

گام به گام فعّالیت صفحه 2 درس 1 ریاضی نهم (مجموعه ها) را در سایت تک متن آماده کرده ایم. این پاسخ ها همگی برگرفته از کتاب گام به گام هستند. در ادامه با ما باشید.

در شکل رو به رو شمارنده های طبیعی عدد ٦٠ را نوشته ایم و بین آنها شمارنده های اول را مشخص کردهایم. شما هم شمارنده های ٦٠ را که اول نیستند، در یک منحنی بسته قرار دهید.

اگر شمارنده های طبیعی و او ِل عدد 50 یعنی 2، 3 و ٥ را در داخل دو آکلاد قرار دهیم و آن را با حروفی چون  A یا B یا … نام گذاری کنیم و بنویسیم {5، 3، 2} = A؛

در این صورت یک مجموعه تشکیل دادهایم و به هریک از عددهای 2، 3 و ٥ یک عضو مجموعه A می گوییم؛ پس مجموعه A دارای 3 عضو است.

٭ شما شمارنده های مرکب عدد ٦٠ را به صورت یک مجموعه بنویسید و آن را B بنامید.

٭ مجموعه شامل شمارنده های عدد ٦٠ که نه اول باشند، و نه مرکب، چند عضو دارد؟ این مجموعه را نیز C بنامید و آن را نمایش دهید.

٭ مجموعه D شامل همه شمارنده های دو رقمی ٦٠ را تشکیل دهید؛ این مجموعه چند عضو دارد؟

از رضا و احمد خواسته شد تا مجموعه شامل 3 شمارنده زوج عدد 60 را تشکیل دهند. احمد نوشت: {10، 6، 4} رضا نوشت: {12، 10، 6} نظر شما چرا جواب های آنها با هم فرق دارد؟

نتیجه: در ریاضیات عبارت هایی شبیه این عبارت، که مشخص کننده ٔ یک مجموعه معین و یکتا نباشد، مجموعه ای را مشخص نمی کند.

قسمت اوّل)

n(B) = 8 ، مطابق شکل زیر مجموعه ها را متمایز می کنیم:

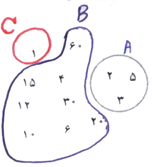
قسمت دوم)

n(c) = 1

قسمت سوم)

D = {60, 10, 30, 15, 12, 20}    →    n(D) = 6

قسمت چهارم (علّت تفاوت جواب های رضا و احمد) :

چون عدد شصت، 8 شمارنده ی زوج دارد و رضا و احمد به سلیقه ی خود و به دلخواه می توانند سه عضو از آن را انتخاب کنند

شمارنده های زوج عدد 60 :

{60 و30 و20 و12 و10 و6 و4 و2}

برای انتخاب اولین عضو (8 حالت) و برای عضو دوم (7 حالت) و برای عضو سوم (6 حالت) داریم پس

کل انتخاب ها برابر است با (336 = 6 × 7 × 8)

می دانیم ترتیب نوشتن اعضاء در یک مجموعه تاثیری ندارد یعنی داریم

{2، 4، 6} = {2، 6، 4} = {4، 2، 6} = {4، 6، 2} = {6، 2، 4} = {6، 4، 2}

لذا هر مجموعه 6 بار تکرار می شود بنابراین داریم

تعداد زیرمجموعه های سه عضوی از 8 عضو: 

\(\frac{{8 \times 7 \times 6}}{6} = 56\)

نکته ی مهم: چون عنصر های یک مچموعه متمایز هستند، لذا {a, a, b} نماد مناسبی برای مجموعه {a, b} نیست